Tak a je to tu... nie je to tak obsiahle, pretože to by som písal ešte dlho o veľa veciach a zamotal by som sa
Že rýchlosť svetla je základnou a fundamentálnou konštantou, vie už skoro každý. Známa špeciálna teória relativity, ktorú v roku 1905 publikoval Einstein, hovorí, že nič sa nemôže pohybovať rýchlejšie ako svetlo. Dokonca nie je ani možné dosiahnuť túto rýchlosť, čiže všetky hmotné objekty (objekty, ktoré majú nenulovú pokojovú hmotnosť) nikdy nedosiahnu rýchlosť svetla, ktoré značíme symbolom „c“. Hodnota tejto konštanty predstavuje presne 299 792 456 metrov za jednu sekundu. Platí samozrejme len vo vákuu, kde svetlo nemá v ceste žiadnu prekážku.
Pred pár týždňami svetom, tak trošku senzačne, prišla správa o tom, že ŠTR (špeciálna teória relativity) asi neplatí, pretože Neutrína zrejme prekonali túto rýchlosť. Samozrejme, tieto média bez hlbšieho vysvetlenia situácie to bez problémov publikovali. Široká verejnosť tak potom začne šíriť senzačné správy o tom, že Einstein sa mýlil. Niečo také si netrúfajú povedať ani tí najlepší vedci, pretože výsledky mohli byť chybné. Veď nie je ani dôvod predpokladať, že ŠTR by nemala platiť. Na overovanie výsledkov budeme čakať ešte dlho. My si dnes aspoň môžeme jednoducho vysvetliť, prečo by sme nemali Einsteinovú teóriu hneď „odpisovať“ a prečo nám už viac ako sto rokov slúži tak dobre, bez jedinej chyby.
Čo je to Špeciálna teória relativity
Einstein pri formovaní teórie tvrdil, že nič sa nemôže pohybovať rýchlejšie ako svetlo a dokonca ani rýchlosťou svetla.Formuloval dva najdôležitejšie postuláty modernej fyziky a to:
1. Princíp relativity – Všetky fyzikálne zákony platia vo všetkých vzťažných sústavách rovnako.
To sa dá vysvetliť jednoducho tak, že ak hodím jednu a tú istú loptu v pohybujúcom sa vlaku a na vlakovej stanici, experiment, resp. to čo uvidím (dopad lopty) dopadne rovnako. Dopadne rovnako rýchlo ako na podlahu vlaku, tak na podlahu miestnej vlakovej stanice. Samozrejme, za predpokladu, že ich pustíme z rovnakej výšky a že ich neovplyvní tlak vzduchu, vietor a ďalšie drobnosti.
2. Konštantná rýchlosť svetla „c“ – Rýchlosť svetla je nemenná vo všetkých vzťažných sústavách pre všetkých pozorovateľov.
To znamená, že bude nemenná pre pozorovateľa, ktorý ide svetelnému lúču naproti alebo mu chce ujsť. Nezáleží, či sme v pohybe alebo stojíme.
Einstein si položil otázku:
„prečo sa každý pozorovateľ vo vesmíre vždy zhodne na úplne rovnakej rýchlosti svetla ?“.
Odpoveď prišla v podobe na tú dobu kontroverzného tvrdenia, že sa musí meniť náš „meter“ a tok vlastného času. Prišiel tak na revolučný objav, že čas nie je absolútny, nemenný, ale že naopak, čas je dynamická veličina. Každému pozorovateľovi plynie čas inak. Špeciálna teória relativity ale prichádza s radou ďalších zaujímavých dôsledkov.
Najslávnejšia fyzikálna rovnica, ktorá sa tak trošku stala aj ikonou fyziky, vzťah medzi energiou a hmotnosťou,
E=mc². Táto jednoduchá rovnica vlastne popisuje chovanie hmoty a energie. Fyzici neoddeľujú hmotnosť a energiu, ale vnímajú ju ako inú stranu tej istej mince. Energia je jednoducho forma hmotnosti, tak ako je hmotnosť forma energie. To znamená, že ak pridávam do systému energiu, tak sa tým pádom zvyšuje aj jeho hmotnosť. S ubúdaním energie hmotnosť klesá. Horúci šálok kávy je nepatrne ťažší ako studený. Dôvod, prečo to ale v každodennom živote nevidieť je ten, že sa to nedá prakticky odmerať, takže to pre bežný život nemá žiadny fyzikálny význam. Na malých merítkach si prakticky vždy vystačíme s klasickými zákonmi a princípmi fyziky objavených pred Einsteinom. Praktické využitie ale nachádza ŠTR vo fyzike vysoko energetických častíc, napríklad v podobe dopadajúcich Pí Mezónov (Mión), ktorých detekciu na povrchu Zeme by sme bez ŠTR, dilatácie času, nevedeli vysvetliť.
Relativita v praxi
Ako sme si už povedali, pohybujúci sa objekt má vždy kratší časový interval tej istej udalosti ako stojaci pozorovateľ. Pí Mezóny majú jednu zvláštnosť a to, že vznikajú vo vrchných častiach atmosféry a dopadajú na zemský povrch rýchlosťou okolo 0.99c. Vtip je ale v tom, že ich doba života je tak malá, že uraziť bezmála 300km od vzniku častice až po zemský povrch by podľa klasickej fyziky nemali stihnúť, pretože sa rozpadnú ešte pred dopadom na zemský povrch. Povedané inou rečou, nemali by sme ich vôbec detekovať a predsa o nich vieme. Vysvetlenie nám dáva ŠTR. Pí Mezónom skrátka beží čas pomalšie.
A preto z nášho pohľadu stihnú doletieť až na zemský povrch. Z pohľadu Pí Mezónov sa zase zdá, že sa im skrátila vzdialenosť (kontrakcia dĺžok) a preto stihli dopadnúť na Zem. Obidva pohľady sú správne a korektné. A práve v tomto tkvie najkrajšia vec na celej ŠTR – princíp relativity. Z princípu relativity pochádza aj jeden (zdanlivý) paradox. Paradox dvojčiat. Mnohí ľudia vidia paradox práve v rýchlejšom starnutí jedného z dvojčiat od druhého. Ale po bližšom skúmaní zistíme, že by podľa ŠTR nemalo ani jedno z dvojčiat zostarnúť práve preto, lebo obidve starnú rovnako rýchlo. Povedali sme si, že neexistuje rozdiel medzi pohybom alebo tým, či stojíme na mieste. To znamená, že dvojča, ktoré sa vzďaľuje relativistickou rýchlosťou od svojho brata na Zemi vidí rovnako, že starne jeho brat, ktorý stojí na mieste, pretože pohyb je relatívny. Práve v tom spočíva kúzlo paradoxu, že jedno z dvojčiat sa vráti predsa len staršie. Odpoveď nám poskytne až OTR. A práve paradox dvojčiat je takou „prestupnou“ stanicou alebo mostom medzi týmito dvoma teóriami.
VTR (Všeobecná teória relativity) narozdiel od ŠTR berie do úvah aj pojem o nerovnomernom pohybe. To znamená, že počíta aj s postupným zrýchľovaním, brzdením a gravitáciou. Nás budú pri paradoxe dvojčiat zaujímať len prvé dva pojmy a to zrýchľovanie a spomaľovanie. Keďže sa pri týchto neinerciálnych pohyboch (nerovnomerne zrýchlených) raketa nepohybuje konštantnou rýchlosťou, čas taktiež nebude plynúť stále konštantne voči stojacemu pozorovateľovi. Raketa tak stále mení svoju rýchlosť a smer pohybu, čo má merateľný dilatačný efekt. Práve to zapríčiňuje zostarnutie jedného z dvojčiat. V princípe sa dá povedať, že energia, ktorú sme dodali do systému, aby sme dosiahli rýchlosť 0,99c spôsobuje relativistické efekty.
Čo sa vlastne deje pri týchto neinerciálnych pohyboch ? Vzniká nám tzv. lokálne gravitačné pole. Princíp ekvivalencie hovorí (základný postulát VTR), že nejde odlíšiť zrýchľujúcu raketu alebo auto (čokoľvek) od gravitačného poľa.
Predstavte si, že stojíte na podlahe rakety. Akékoľvek informácie o vonkajšom svete (aj o tom, či vaša raketa zrýchľuje alebo má vypnuté motory) sú vám neznáme. Dokonca ani neviete, či ste vôbec vo vesmíre alebo niekde na Zemi v servisnom doku. Laik by povedal, že sme celkom určite na Zemi, veď stojíme nohami pevne na podlahe. Hodíme si loptičkou, ktorá taktiež dopadne akoby sme boli na Zemi, dokonca aj moja hmotnosť a energia, ktorú vynaložím na pohyb a výskok v rakete je rovnaká ako na Zemi. Naraz ale zistí, že je vo vesmíre, kde predsa nemôže pôsobiť tak silné gravitačné pole. Preňho to ale nie je žiadna neriešiteľná hádanka, pretože na hodine fyziky dával pozor a vie, že jeho raketa vykonáva zrýchlený neinerciálny pohyb, ktorý je v princípe vždy na nerozoznanie od gravitácie.
Relativistické skladanie rýchlostí
Je dôležité poznamenať, že LIS (lokálna inerciálna sústava) v rakete, ktorá sa konštantne pohybuje v=0,99c sa budú všetky deje chovať tak, akoby raketa stála. Takže zo sústavy spojenej s raketou môžeme urýchliť napríklad nejakú časticu až do v=0,99c. Teraz si predstavme tretieho pozorovateľa, ktorý vidí „roentgenovými“ okuliarmi všetky prebiehajúce deje v rakete a ktorý je spojený zo sústavou mimo rakety a vzhľadom k nej stojí. Laik povie, že sa rýchlosti musia sčítať. Ale v skutočnosti tretí pozorovateľ nenameria súčet rýchlosti rakety a ďalšej menšej rakety ako 0,99c + 0,99c = 1,98c ale stále podsvetelnú rýchlosť v ˂ c.
Ako vieme na relativite a to hlavne špeciálne je krásna jedna vec a to elegantná jednoduchosť s akou popisuje nám známu skutočnosť. Takže vždy existuje vďaka nekonečnému počtu rôznych vzťažných sústav iný tvar popisu tej istej udalosti, kde výsledok experimentu dopadne vždy rovnako. Môžeme sa dohodnúť, že všetky telesá (a nezáleží na smeru, hybnosti atď.) sa pohybujú po priestorovej zložke rýchlosťou c a po časovej rýchlosťou t. Stojacemu pozorovateľovi plynie ale len zložka času t. Telesám v kľude beží vlastný čas vždy najrýchlejšie. Ak sa začnú pohybovať, začne sa pomyslený pomer v/c=1 meniť. Teleso sa pohybuje po priestorovej zložke a aj časovej. Čím rýchlejšie sa pohybuje, tým menej mu zostáva zložka t, čiže sa mi principiálne spomaľuje čas a keď sa pohybuje rýchlosťou 0,99c, tak mu čas beží extrémne pomaly, tak ako naším Pí Mezónom. Proste časť svojej energie musí vynaložiť na pohyb priestorom a to zapríčiňuje dilatáciu času a iné relativistické javy.
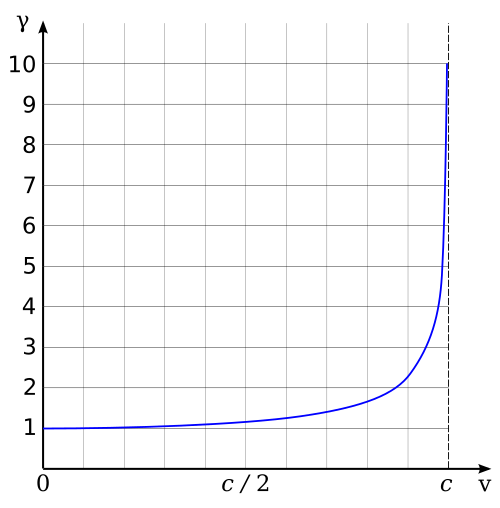
Na to som si vymyslel aj taký vtipný výrok: „Čím viac pracuješ, tým viac času vzdoruješ.“ Prácou W sa myslí energia, ktorú musíme vynaložiť na uskutočnenie nejakého pohybu (práce).
Relativistická dynamika
Relativistická dynamika sa zaoberá dynamickými dejmi, ako hmotnosť, energia, hybnosť a kinetická energia.
Energia je formou hmotnosti (alebo hmoty) a naopak. To vlastne znamená, že energia musí byť relatívna. Ak máme objekt o hmotnosti 1Kg a chceme ho urýchliť. Na urýchlenie potrebujeme vykonať prácu a práca je energia. To znamená, že pri urýchľovaní pridávame tomuto objektu energiu a čím viac tej energie pridávame, tým viac sa zvyšuje aj hmotnosť telesa a je jedno, v akej forme (pohybovej, tepelnej atď.) tá energia bude dodaná.
V relativite preto rozlišujeme pokojovú a relativistickú hmotnosť. Pokojová(vlastná) hmotnosť telesa sa nikdy nemení bez ohľadu nato z akej sústavy objekt sledujeme. Takže hmotnosť zostáva invariantná (nemenná). Takže je veľmi dôležité, si to ujasniť. Na začiatku som zámerne ponechal tento výraz tak, pretože teplo je vnútorná energia (ohrievali sme kávu) a to je energia molekúl/atómov, tá sa dá považovať za súčasť pokojovej hmotnosti šálku kávy. Aj keď sa táto hmotnosť časom zmenší (chladne). Kinetická energia Ek je naproti tomu čisto relatívna veličina a vždy záleží na voľbe vzťažnej sústavy.
Predstavme si to na jednoduchom príklade s dvomi autami, ktoré idú vedľa seba konštantnou rýchlosťou
v.
Obidvom vodičom sa bude zdať, ak sa pozrú na seba, že stoja a namerajú medzi sebou nulovú rýchlosť, aj ich kinetická energia je v ich vzťažnej sústave nulová. V vzťažnej sústave spojenej napríklad s chodcom je už situácia úplne odlišná. Pomocou prístroja na meranie rýchlosti zistí, že autá sa smerom k nemu pohybujú určitou rýchlosťou, takže majú aj určitú kinetickú energiu. Toto isté sa dá transformovať aj o relativistickej hybnosti, kde si ale vysvetlíme jednu zaujímavosť, ktorá súvisí so svetlom.
Má alebo nemá ?
O fotónoch sa hovorí, že sú nehmotné. Čo samozrejme nie je pravda. Treba si uvedomiť, že fotóny musia mať vždy nejakú hmotnosť, ktorá závisí od ich
E (Energia). Slovíčko vždy treba zdôrazniť, pretože fotón v pokoji nemá žiadnu hmotnosť, čo sa pravdepodobne prejavilo na občas mylnej (aj ja som bol zasiahnutý) interpretácii, že fotón je nehmotný. Nehmotný fotón ale nemôže existovať, inač povedané, fotón v pokoji zaniká. Energiu fotónu vyjadríme jednoduchou rovnicou
E=h*f
Kde E je celková energia, h je plancková konštanta a f je frekvencia. Z tohto vzorčeku Vám musia byť jasné dva veci.
Za prvé pri nulovej frekvencii f nám energia E vychádza rovná 0. E=h*0 = 0. Druhá skutočnosť súvisí s Dopplerovým javom. Vieme, že energia/hmotnosť je relatívna (ukázali sme si to na príklade áut a chodca). To isté platí aj pre frekvenciu (a tým pádom aj energiu) fotónu.
Ak sa žiarič pohybuje smerom k detektoru, zachytíme vyššiu frekvenciu (energiu) prichádzajúcich fotónov ako keď sa bude žiarič od detektoru vzďaľovať (musí platiť, že detektor alebo žiarič sa pohybujú nerovnomerne zrýchlene). Predstavte si, že hádžeme tenisovú loptičku rýchlosťou 2m/s do meter vzdialenej steny a hneď po obdržaní loptičky ju (bez latencie) hodíme na stenu a ona sa nám bude periodicky stále vracať. Frekvencia dopadu na stenu bude 1hz (1 loptička za jednu sekundu, počítame f od detekcie na stene po ďalšiu detekciu na stene).
Ak zachováme rýchlosť hodov na stenu ale skrátime ich vzájomnú vzdialenosť zistíme, že frekvencia sa nám zvýšila. Skráťme teda vzdialenosť steny a nášho nadhadzovača o 0,5m, čiže o polovicu. Túto vzdialenosť nám prejde loptička za
0,5s. Frekvencia teda vychádza vyššia a to
1/T kde T je perióda 0,5s (od steny k stene). Takže
1/0,5=2hz Vyšlo nám teda, že za stále rovnakú referenčnú jednotku času 1 sekunda, sa loptička dotkne steny 2 krát a preto hovoríme dva loptičky za jednu sekundu.
Tak to je všetko, pýtajte sa poprípade opravte mňa, kľudne som sa mohol na nejakej banalite
.